Chapter 3 — The Fourth Dimension (D4): The Hidden Foundation of Reality
How a hidden geometric substrate (D4) makes structure inevitable.
Chapter 1 asked the oldest question: Why does anything exist?
Chapter 2 revealed the first event: the first symmetry break.
Now we uncover the deeper truth beneath both
Where did that first event occur?
Creation requires a “place” — not a location in space, but a deeper foundation in which instability can arise and become structure.
Not space.
Not time.
Not matter or energy.
Before all of that —
there is D4.
D4 — The Fourth Dimension
D4 is not time (as commonly taught).
It is not a parallel universe.
It is not “another place” sitting beside our own.
D4 is the foundational geometric substrate from which spacetime emerges.
Spacetime is not the stage.
Spacetime is the product.
D4 is the hidden foundation that makes structure possible at all.
What D4 Is
D4 is best understood as a baseline — a perfectly uniform deeper-dimensional substrate.
It is:
- uniform
- structureless
- directionless
- distance-free
A perfectly balanced geometric condition.
Not emptiness.
Not a vacuum.
A pre-geometry — where geometry has not yet formed.
And yet D4 has one crucial property — the property that makes existence possible:
D4 can be stable enough to exist… but not stable enough to remain perfectly uniform forever.
That subtle instability is the seed of everything.
Why D4 Must Exist
Absolute nothingness could never:
- change
- move
- oscillate
- curve
- create structure
Perfect nothing has no mechanism for difference, no framework for comparison, no way to allow transition.
So if the universe exists, it could not have emerged from perfect nothing.
It must have emerged from something that is almost nothing —
but not perfectly nothing.
D4 is exactly that.
It appears empty — because it contains no objects —
yet it contains the one requirement that “nothingness” cannot contain:
a built-in vulnerability in perfect symmetry.
The Key Property of D4
In D4, a “point” has no defined scale.
It can represent the infinitely small and the infinitely large simultaneously —
not because it contains infinity as a substance,
but because scale has not yet been born.
A point with no defined extent cannot anchor a fixed identity.
And without fixed identity:
- symmetry cannot be permanently enforced
- perfect equilibrium cannot be permanent
- uniformity cannot remain unbroken
So even if D4 begins perfectly uniform…
it cannot remain that way forever.
This is not randomness.
It is not a disturbance from outside.
It is a geometric inevitability:
perfection cannot hold in a substrate with no scale.
And when symmetry breaks —
curvature is born.

Figure 3.1 — The First Curvature
A tiny perturbation in the D4 substrate stabilizes into a dome of curvature. For the first time in existence, there is an inside and an outside. Structure — and the path to time — has begun.
Once symmetry breaks, distortion appears in the only form a pre-geometry can express:
as curvature.
And because D4 has no directions in space, the earliest motion is not “left” or “right,” “up” or “down.”
Instead, it appears as the two fundamental modes of curvature:
- inward— curving into itself
- outward— curving away from itself
These are not spatial directions.
They are the earliest possible geometric responses of a uniform substrate losing perfect balance.
Where inward and outward curvature interact, curvature can loop.
And when curvature loops, something revolutionary happens:
a distortion becomes self-confined.
A crucial implication follows: once the boundary forms, the interior cannot simply “settle” into stillness.
Curvature must continue as a stable dynamic pattern — not random turbulence, but a persistent oscillation.
In later chapters we show that the simplest long-lived structure consistent with the evidence is a two-phase standing curvature oscillator (a breather) confined by the shell — an internal engine whose stable rhythm generates and sustains the external curvature field.
A region of stability forms.
A structure exists.
In physical language, the first structure is:
a self-stabilizing curvature soliton
In STB Theory language, it is:
the first proto-bubble — the seed of all future spacetime bubbles
This is the first “inside vs. outside.”
The first somewhere within something.
Why D4 Makes the Universe Coherent
Once D4 is recognized, many long-standing mysteries shift from unanswerable to structured:
- What existed before the Big Bang?
D4 did. - Why does spacetime curve at all?
Because spacetime emerges from curvature stabilized inside D4. - Why do particles behave like stable objects?
Because they are stabilized curvature patterns. - Why does rotation appear everywhere in nature?
Because rotational shear is a stabilizing mechanism at the birth of structure. - Why is information persistent?
Because curvature can imprint and store configuration. - Why does time flow forward?
Because a boundary creates history — an interior that cannot perfectly reverse into the exterior.
The universe becomes coherent once we stop assuming spacetime is fundamental.
The Cosmic Sequence That Follows
Once the first STB emerges:
curvature → geometry
geometry → particles
particles → atoms
atoms → stars
stars → planets
planets → life
life → consciousness
Everything inherits the deeper structure beneath it.
All existence traces back to curvature forming inside D4.
Why Creation Was Inevitable
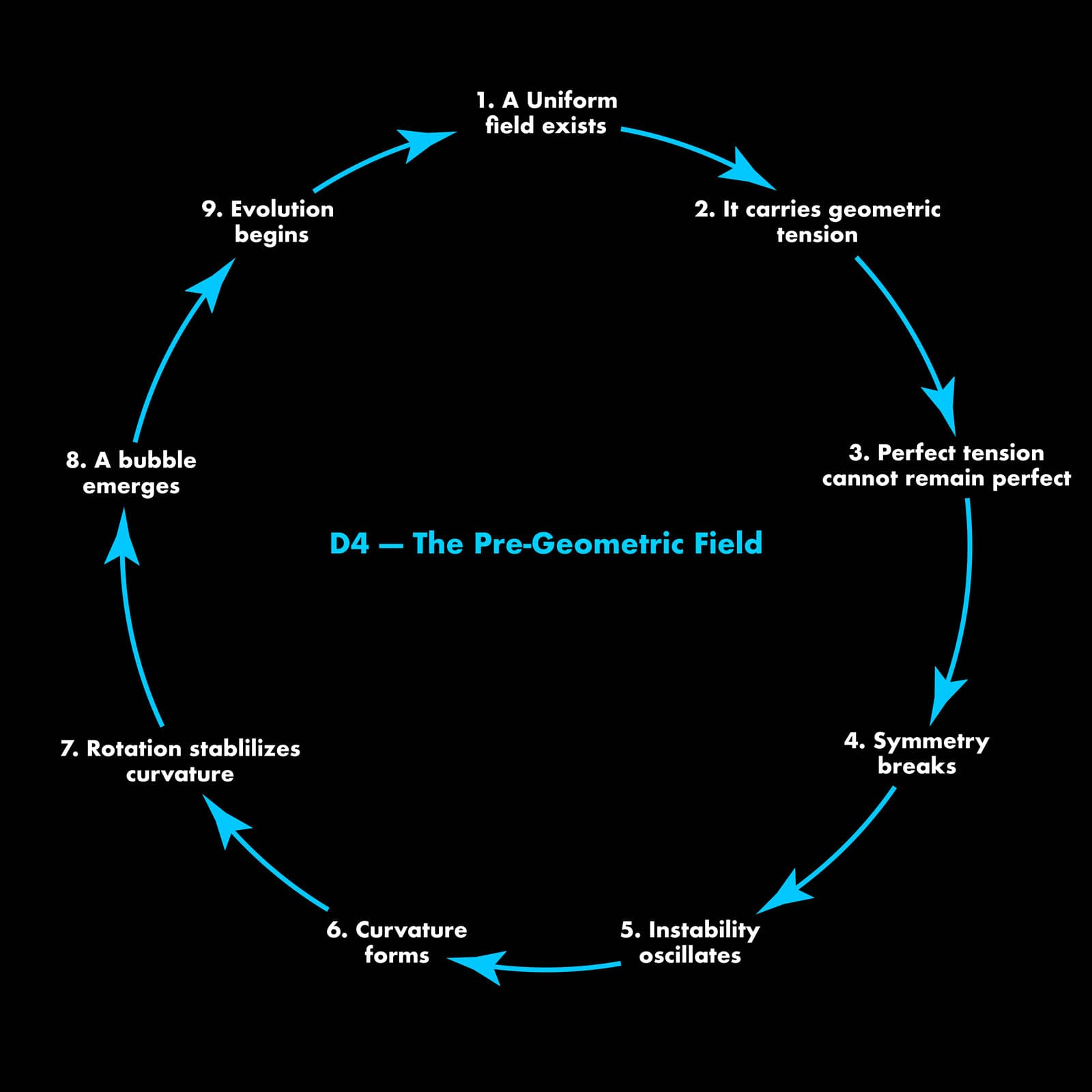
- A uniform substrate exists
- It carries geometric tension
- Perfect tension cannot remain perfect
- Symmetry breaks
- Instability oscillates
- Curvature forms
- Rotational shear stabilizes curvature
- A bubble emerges
- Evolution begins
No magic.
No exceptions.
No metaphysics.
Existence happens because the foundation of reality cannot remain perfectly still.
Chapter 3 in One Sentence
D4 is stable enough to exist but not stable enough to remain perfect — and that subtle instability becomes everything.
Chapter 3 — Technical Notes and Clarifications
This appendix provides clarification for several foundational concepts introduced in Chapter 3.
Its purpose is not to argue, but to ensure that key terms are understood precisely before the theory advances to its first mechanisms in Chapter 4.
Clarification 1: The Meaning of “Dimension” in D4
In this work, a “dimension” does not refer to an additional spatial direction embedded within familiar space.
D4 is not a higher spatial axis that objects move through or perceive.
Rather, D4 refers to a deeper geometric degree of freedom — a continuous substrate capable of supporting curvature, tension, and closure — from which spacetime itself emerges.
Spacetime is therefore not four-dimensional in the conventional sense inside D4.
It is a stabilized structure that forms from D4.
Clarification 2: “Infinitely Small and Infinitely Large” Is Not a Physical Size Claim
The statement that every point in D4 is both infinitely small and infinitely large is not a claim about physical size.
It is a statement about scale indeterminacy.
A point in D4:
- has no fixed extent
- has no minimum or maximum scale
- cannot anchor a defined identity
Because scale is undefined, perfect symmetry cannot be permanently maintained.
This instability is geometric, not energetic.
Clarification 3: Infinity Is Used as a Limit, Not a Substance
Infinity is not treated as a physical object or measurable quantity in this framework.
It is used in the mathematical sense of a limit condition — indicating the absence of imposed bounds.
D4 does not “contain infinity.”
Rather, it lacks intrinsic scale constraints.
This distinction is essential to understanding why symmetry cannot remain perfect.
Clarification 4: D4 Is Not a Metaphysical Assumption
D4 is introduced as the minimum geometric condition required for the emergence of structure.
No assumptions are made regarding:
- matter
- energy
- time
- forces
- particles
All such concepts appear only after curvature stabilizes.
D4 is therefore not metaphysical speculation, but a proposed pre-physical geometric condition.
Clarification 5: Why Perfect Symmetry Cannot Persist
A point with no defined size cannot maintain a fixed state.
Without scale, without boundaries, and without external reference:
- identity cannot be anchored
- symmetry cannot be enforced
- equilibrium cannot be permanent
Loss of perfect symmetry is therefore not caused by randomness or disturbance.
It is an inevitable consequence of geometric indeterminacy.
Closing Note
Chapter 3 establishes the conditions under which curvature must arise.
Chapter 4 examines what happens when it does.
The transition from symmetry to curvature is not an event in time —
it is a geometric inevitability.
© 2025 Michael “Blair” Hopper. All Rights Reserved.

