Chapter 2 — The First Symmetry Break
How perfect symmetry fractured — giving rise to curvature, structure, and time.
In Chapter 1, we established S0 as the baseline of absolute nothingness and examined the conditions under which perfect uniformity cannot persist. In this chapter, we show how that instability leads to the formation of the first stable structure — a Spacetime Bubble (STB).
If Chapter 1 asked the question,
then Chapter 2 delivers the first real answer.
To understand how existence began, we must understand the one event that makes creation unavoidable:
the first symmetry break.
Before anything existed — before space, before time, before matter — reality was not empty. It was deeper than emptiness.
No particles.
No energy.
No motion.
No direction.
No boundaries.
Not even “emptiness” in the way we usually imagine it.
In Chapter 1 we defined the true starting point: S0 (S-Zero) — absolute nothingness, with one unavoidable requirement: it must be capable of instability.
But once instability exists, S0 cannot remain purely undefined. The first consequence of instability is the emergence of the earliest possible substrate — a uniform deeper-dimensional baseline that is stable enough to exist, yet not stable enough to remain perfect.
This is D4 — and once it exists, the symmetry break is no longer a question of if — only when.
Why D4 Appears at All
It may seem like we are introducing D4 too quickly — as if it were an added assumption. But D4 is not an invention. It is the first stable consequence of instability.
When a system cannot remain perfectly uniform, it must do something — not because it is pushed, but because instability cannot stay “featureless.” The moment uniformity becomes even slightly unstable, the system naturally collapses into the simplest stable form available.
This is not mysterious. We see the same kind of inevitability everywhere in nature:
Humidity condenses into droplets.
Supercooled water snaps into ice.
A perfectly tensioned surface forms ripples.
When stability is violated, structure appears as the system’s attempt to settle into the lowest-tension state.
D4 is the same kind of emergence: the first equilibrium-like substrate that S0 can settle into once perfect nothingness becomes unstable.
It is the minimal geometry that can exist — stable enough to persist, unstable enough to break.
It had no structure, no geometry, no inside or outside. Nothing could be measured. Nothing could be compared. Nothing could be defined.
And yet, one fact must be true:
S0 could not remain perfectly uniform forever.
And the moment perfect uniformity fails, the first structured baseline appears: D4.
That is the defining property.
If perfect uniformity were stable forever, existence could never begin.
But if uniformity is even slightly unstable — if symmetry cannot be anchored indefinitely — then creation becomes inevitable.
Because the first time symmetry fails, something new appears:
difference.
And difference is the first ingredient of structure.
What We Mean by “Curvature”
Curvature here refers to how much a geometric region bends or twists as it deviates from perfect uniformity.
In simple geometric terms, curvature measures “how sharply something bends” — much like how a curved road changes direction more than a straight one.
Phase I — The Symmetry Break
• Perfect uniformity in D4 becomes unstable and begins to distort
In the earliest state, D4 is featureless. It has no preferred direction because nothing has happened yet to distinguish one direction from another. It is not “flat space,” because space does not yet exist. It is simply the baseline: a perfectly uniform substrate.

Figure 2.1 — The Uniform Substrate Before Disturbance
Reality began as a perfectly uniform deeper-dimensional substrate — no direction, no geometry, no time, no information — only the potential to become unstable.
This is the most important point:
In a perfectly uniform substrate, nothing can begin unless symmetry fails.
There is no “cause,” no “force,” no “push.” There is only the unavoidable fact that perfect identity cannot hold forever.
So the first moment is not a bang.
It is not an explosion.
It is a break.
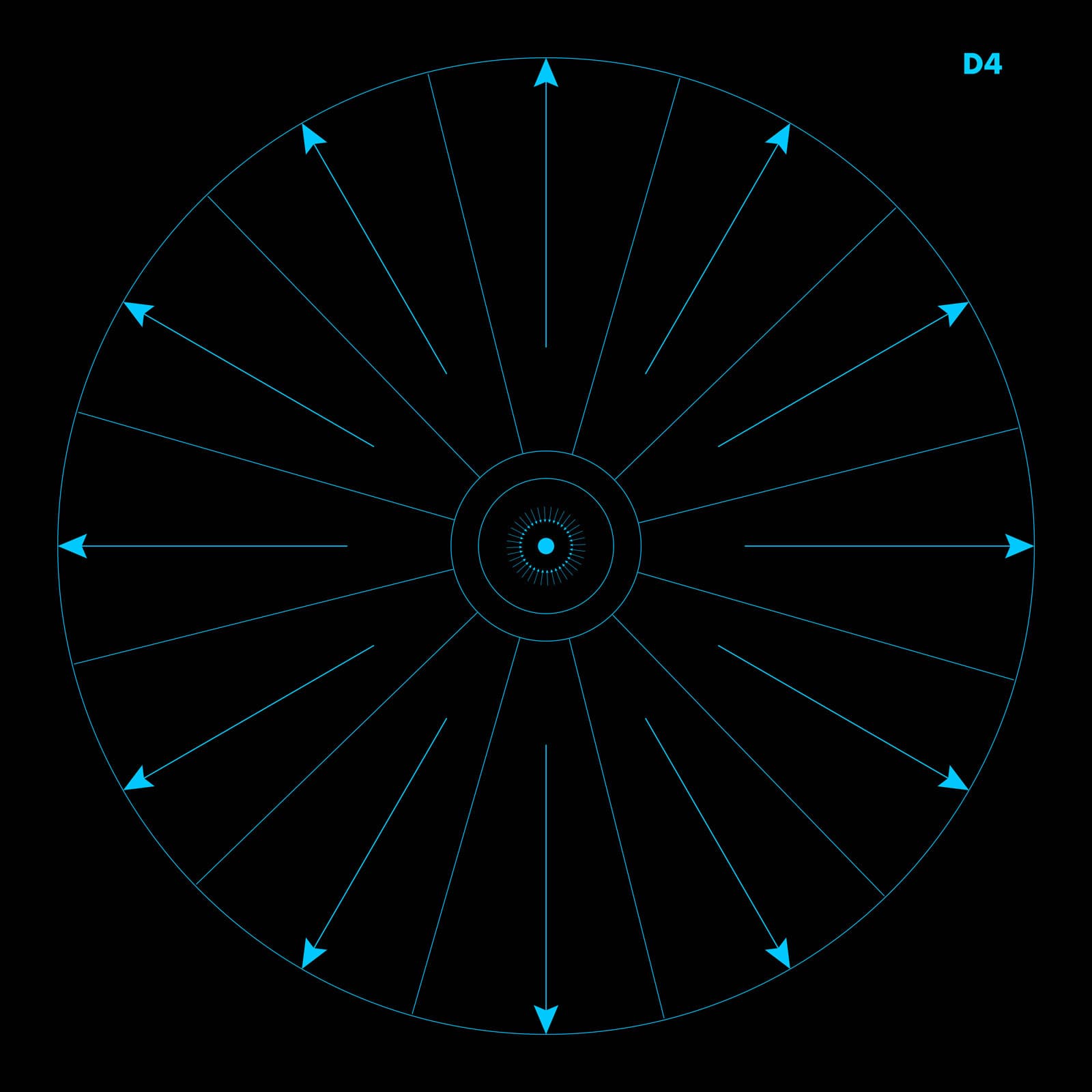
Figure 2.2 — The Uniform D4 Field
A perfectly uniform deeper-dimensional substrate with no preferred direction, no structure, and no geometry — the baseline before the first disturbance.
Once symmetry breaks, motion becomes possible — not motion through space, but motion in relation. The substrate can now experience imbalance.
And in D4, all possible imbalance reduces to two fundamental behaviors:
- inward
- outward
These are not forces yet. They are simply the first two geometric tendencies available to a uniform system that has lost perfect symmetry.
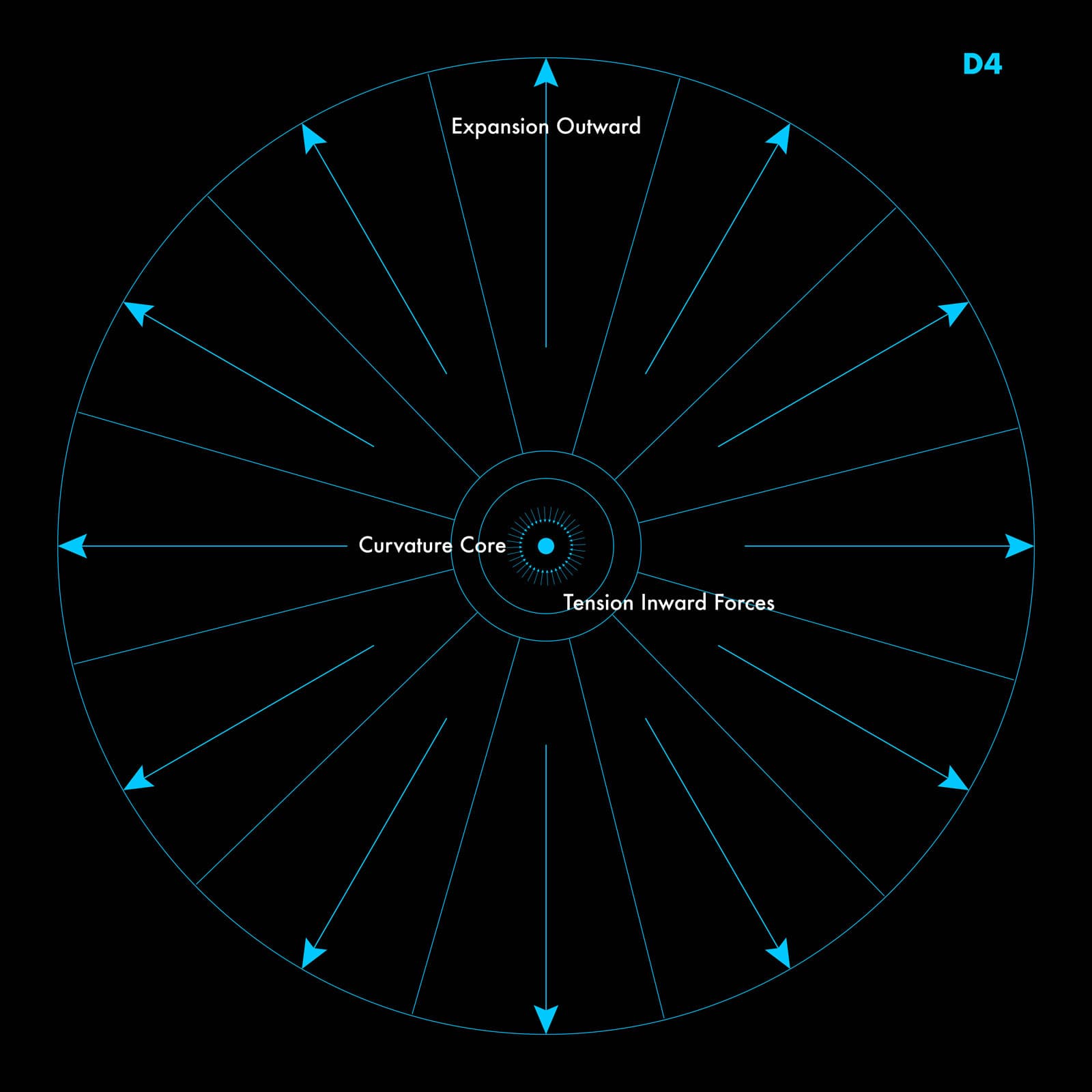
Figure 2.3 — Inward–Outward Motion Produced by Symmetry Break
The first oscillation creates opposing tension behaviors: inward contraction and outward expansion. This is the earliest geometric motion in reality.
At first, inward and outward motion would simply oscillate — rise and fall — and then dissolve back into uniformity. But symmetry has already failed, and D4 has no mechanism to “reset” to perfection.
So the system does what all constrained continua do:
it begins to shear (a twisting distortion that prevents simple collapse).
Shear is crucial, because it prevents immediate collapse. Shear creates circulation. It creates persistence. It makes curvature dynamic rather than temporary.
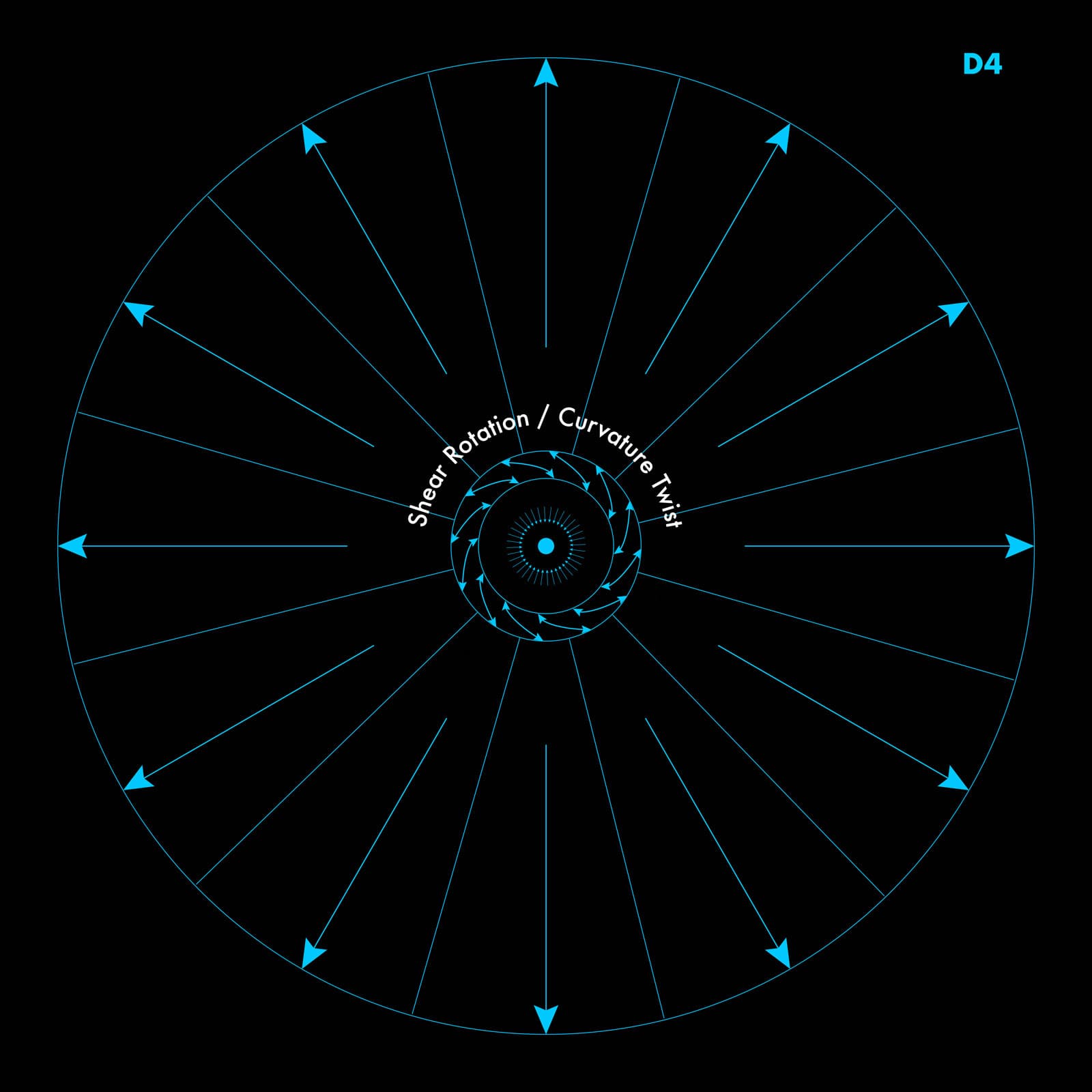
Figure 2.4 — Shear Rotation: How Curvature Becomes Dynamic
When contraction and expansion combine with rotational shear, curvature no longer collapses — it stabilizes into a coherent, persistent structure.
Phase II — Boundary Emergence
• A distinction forms between an interior region and its surroundings
Once shear exists, the substrate no longer behaves as a simple oscillation. The distortion becomes asymmetric. Gradients begin to form. In certain regions, curvature intensifies.
At this stage, a new concept begins to appear:
a boundary.
Not a physical wall.
Not a membrane (a stabilized boundary formed by locked curvature)
.
Just the first detectable separation between inside-like behavior and outside-like behavior.
This is the first time reality begins to create structure.
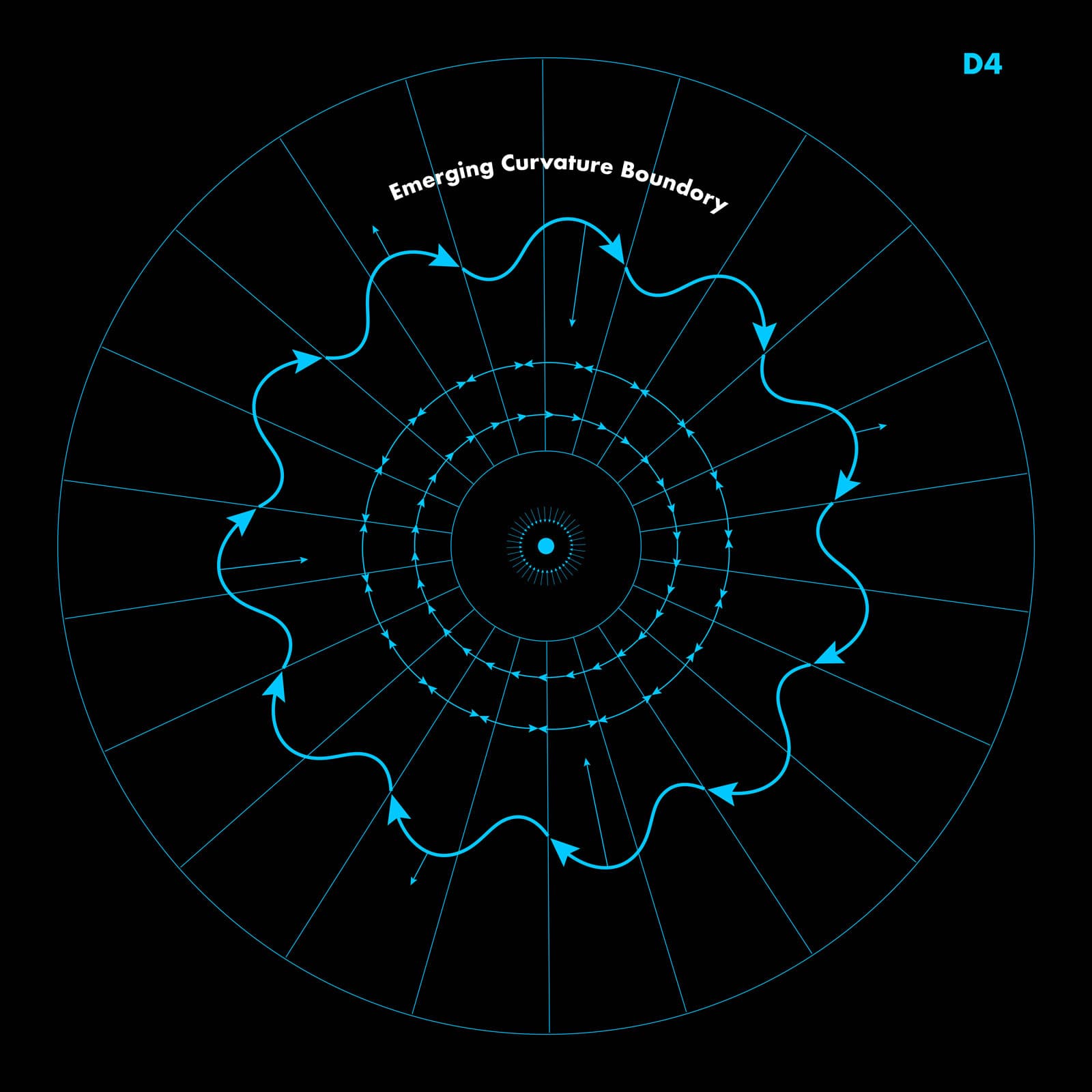
Figure 2.5 — Emerging Curvature Boundary (V4)
As rotational shear increases, the first geometric consequence appears: a visible curvature boundary emerges.
The once-uniform D4 field now displays uneven distortions. These distortions form a wavy, unstable outline — the earliest sign that “inside” and “outside” are no longer equivalent.
A curvature gradient now exists. Symmetry has failed locally. Instability is now feeding geometry.
Once a boundary begins to form, it changes everything.
A boundary introduces geometry that can “hold” distortion. Once distortion can be held, curvature can begin to concentrate. And when curvature concentrates, it begins to behave as directed flow.
This is the first true selection of a location — the first “somewhere” being chosen by geometry itself.

Figure 2.6 — Curvature Collapse Toward Proto-Bubble (V5)
Shear and curvature now act in a coordinated way. The distortions that once oscillated freely begin to collapse inward.
For the first time, curvature flows toward a central region — selecting a specific geometric location.
This is the first true collapse, not gravitational, but geometric. D4 is reshaping itself, funneling curvature into what will become the proto-bubble.
This is the first true selection of a location — the first “somewhere” being chosen by geometry itself.
As curvature collapses inward, the system approaches a turning point:
either the structure dissolves back into uniformity…
or the boundary begins to stabilize.
And here we reach one of the most important truths in the entire theory:
stability is not imposed from outside. It is an outcome of curvature seeking lower tension.
The boundary begins to smooth. Irregularities diminish. The system finds a more coherent outline.

Figure 2.7 — Boundary Stabilization Phase (V6)
The chaotic early boundary begins to settle. Irregularities diminish as curvature redistributes into a more coherent form.
A continuous outline forms — still imperfect, still dynamic, but significantly more stable than before.
A stable geometric container is emerging. Order is beginning to grow from disorder by the natural tendency of curvature to seek a lower-tension configuration.
As stabilization increases, the boundary thickens. Curvature stress concentrates along a layer — and for the first time the boundary becomes more than an outline.
It becomes a proto-surface.
A skin.

Figure 2.8 — Membrane Formation Layer (V7)
A distinct membrane begins to appear. No longer just a wavy outline, the boundary now thickens as curvature stresses concentrate along a specific geometric layer.
This is the first moment when interior and exterior truly separate. D4 is constructing a container — the surface where information will one day persist.
The proto-bubble is acquiring the first version of a “skin.”
Phase III — Membrane Lock-In and Closure
• Curvature stabilizes into a sealed, self-sustaining structure
As the membrane thickens, it reaches a threshold where the system can no longer freely fluctuate back into uniformity.
This is the decisive transition:
lock-in.
At lock-in, the boundary becomes robust enough to persist. The geometry hardens into a self-maintaining shape.
Existence is no longer tentative.
Existence is committed.

Figure 2.9 — Membrane Lock-In Phase (V8)
The membrane geometry locks in. Distortions flatten and smooth. The boundary becomes robust — no longer fluctuating freely, no longer at risk of tearing or dissolving.
Once the membrane locks in, the system can no longer return to its pre-bubble state. Existence is now committed.
Once a membrane exists, geometry begins seeking its lowest-energy closure.
This is why the sphere appears naturally — not as an assumption, but as an inevitability.
A sphere is not merely a shape.
It is the most stable solution for bounded curvature.

Figure 2.10 — Geometric Convergence Phase (V9)
The structure rapidly converges toward a sphere. Internal flows harmonize. Surface tension distributes uniformly. Curvature pathways settle into minimal-energy configurations.
This is the universe’s first moment of true coherence. The geometry is nearly complete.
At final closure, the boundary becomes complete. Inside and outside are now truly separated. The structure is sealed.
What began as the smallest disturbance is now a stabilized container of curvature:
the first Spacetime Bubble (STB).

Figure 2.11 — Spherical Closure Phase (V10)
The membrane fully closes. The last irregularities vanish as geometric tension resolves into spherical symmetry around a central axis of curvature.
What began as a microscopic perturbation is now a sealed, self-stabilizing STB — the first persistent structure in reality.
Not an explosion… but a geometric completion. A transition in curvature, not a blast of matter.
At the moment the bubble seals, reality possesses something it never had before:
- a curvature boundary
- a defined interior
- a defined exterior
- a persistent tension field
- a stable geometry capable of storage
For the first time in history, a structure can persist, record, and evolve.

Figure 2.12 — The First Complete Structure (STB: Inside/Outside Defined)
With the bubble sealed, the system now has an interior and exterior, separated by a stable curvature boundary.
This is the true moment of creation — not the Big Bang as commonly portrayed, but the formation of the first stable region capable of supporting everything that follows.
But the deepest consequence comes next.
Once the membrane closes, internal curvature can no longer fluctuate freely. The oscillations that formed the bubble now imprint themselves into the internal geometry.
This is the first moment structure can store information

Figure 2.13 — First Internal Curvature Imprint (The First Memory Layer)
Once the membrane fully closes, internal curvature no longer fluctuates randomly. The earliest oscillations — the same motions that formed the bubble — leave a permanent imprint on interior geometry.
A STB is not just a stable structure — it is the first object in reality capable of remembering.
The First Structure Did Not Explode — It Assembled
The first Spacetime Bubble did not explode into existence.
It assembled itself through geometry.
A symmetry break created motion.
Motion created curvature.
Curvature created a boundary.
The boundary closed, stabilized — and then, for the first time in the history of reality — began to remember.
From this single geometric transition inside D4, the universe inherits its most fundamental properties:
structure, persistence, rotation, energy, and the capacity for information.
Nothing more exotic was required.
Once a bubble could form, stabilize, and store its own internal imprint, the rest of creation became not merely possible — but inevitable.
Every star, every atom, every planet, every lifeform, every moment of consciousness traces its ancestry back to this first stabilized pocket of curvature — the moment geometry learned to hold its shape.
Creation did not erupt.
It unfolded — one curve at a time, one memory at a time — from absolute symmetry to the first spark of complexity.
Why This Matters
• This is the first time the universe contains an “inside” and “outside”
• Stable boundaries make persistence possible
• Information can now be stored in geometry
• All later particles and forces build on this structure
Curvature isn’t just something matter creates. Curvature is what matter is.
Clarification
Chapter 2 presents a geometric sequence of formation, not a timeline of physical events.
Terms such as “collapse,” “energy,” and “stability” are used descriptively, not in their later physical meanings.
The mechanisms by which these geometric processes give rise to familiar forces and particles are developed in subsequent chapters.
With the first stable spacetime bubbles in place, the universe is now capable of forming internal structure — the subject of Chapter 3.
© 2025 Michael “Blair” Hopper. All Rights Reserved.

