Chapter 4 — How D4 Generates Curvature
In Chapter 3 we showed that D4 cannot remain perfectly uniform; here we explain how that fundamental instability produces curvature — the universe’s first geometric motion.

Figure 4.1 — D4: The Still Foundation Before Curvature
Before any structure, time, or matter can exist, reality rests as a uniform deeper-dimensional substrate. D4 appears perfectly calm — but perfect symmetry cannot hold forever. This is the silent baseline from which the first curvature must emerge.
With D4 defined, the question becomes unavoidable: what does a uniform substrate do when perfect symmetry fails?
It does the only thing it can do — it curves.
D4 is a uniform, deeper-dimensional substrate — stable enough to exist, yet not stable enough to remain perfect.
In Chapter 3 we uncovered its defining property:
Every point in D4 is both infinitely small and infinitely large.
A point with no defined size cannot hold a fixed identity.
It cannot anchor itself.
It cannot sustain perfect symmetry forever.
That single limitation is what allows motion to appear.
And within D4, every possible motion reduces to just two behaviors:
- inward
- outward
These are the seeds of curvature — the fundamental geometric movement from which all physics arises.
Why Curvature Is the Only Possible Response
Imagine a perfectly flat, perfectly uniform sheet stretched in all directions.
If the sheet were flawless, nothing would ever move.
But if the sheet carries tension — and can be disturbed — then every imbalance produces a single universal response:
the sheet curves.
Not because something pushes it.
Not because a force acts on it.
But because curvature is the only way a uniform tensioned field absorbs imbalance.
D4 behaves the same way.
Once a single point loses perfect symmetry —
even by the smallest conceivable amount —
the D4 field responds by curving inward and outward around that disturbance.
This curvature is not an analogy.
It is the first geometric act of the universe.
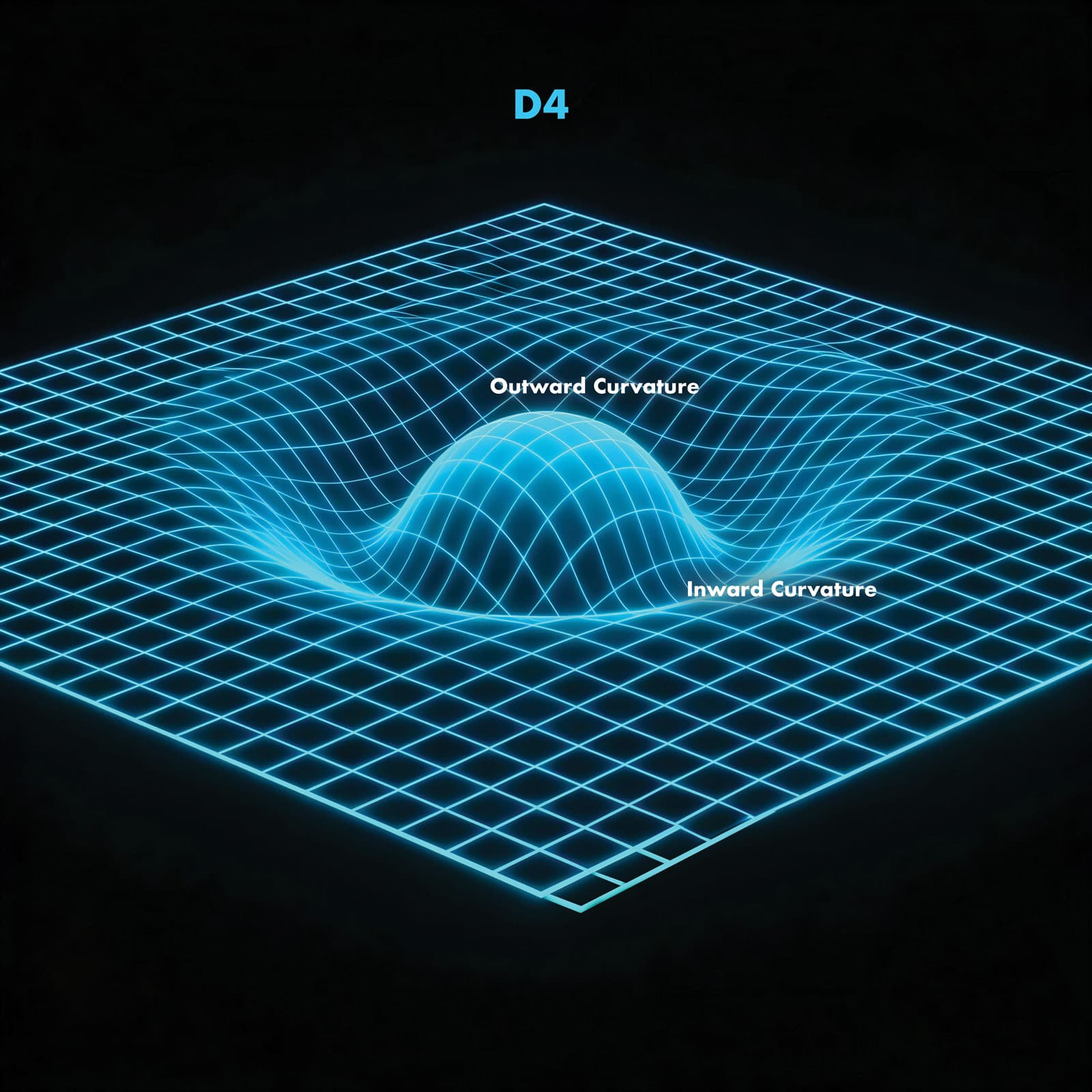
Figure 4.2 — Inward and Outward Curvature
A perfectly uniform D4 field responds to the smallest loss of symmetry by curving both inward and outward around the disturbed point. This is the first geometric reaction in the universe — the seed of all future structure.
Inward Curvature: The First Motion Toward Structure
When a region of D4 contracts inward, the surrounding field follows because:
- the field is continuous
- the field carries tension
- curvature is the natural restoring mode
This produces compression — the first localized collapsing motion.
Inward curvature represents:
- the first tightening of geometry
- the first center
- the first differentiated region
Without inward curvature:
- no particles
- no atoms
- no stars
- no structure of any kind
Nothing could cohere.
Inward curvature is the universe’s first step toward forming something.
Outward Curvature: The First Motion Away From Structure
But inward motion alone cannot stabilize anything.
If contraction were the only behavior, collapse would continue indefinitely.
D4 does something more elegant:
When one region contracts inward, the surrounding regions expand outward.
Outward curvature produces:
- expansion
- rebound
- separation
- the first outward definition of space
Together, inward and outward curvature create an oscillation —
the simplest natural behavior of any disturbed continuous field.

Figure 4.3 — Oscillation Around a Curvature Disturbance
When a symmetry break occurs in the D4 field, curvature does not remain static.
It oscillates — contracting inward, expanding outward, then repeating — creating the first rhythmic pattern in the universe. This oscillation is the precursor to all stable geometric structures, including the first spacetime bubble.
Oscillation: The First Rhythmic Geometry
Imagine pulling a spring and releasing it.
It oscillates.
Now imagine that spring:
- has no edges
- has no friction
- has no time
- exists inside a four-dimensional geometric field
It would oscillate indefinitely — unless stabilized into a new structure.
This is D4.
Oscillation is its natural behavior:
inward → outward → inward → outward
contraction → expansion → contraction → expansion
Once oscillation begins, curvature locks into a persistent repeating pattern.
And repeating curvature becomes the blueprint of a bubble.
Curvature Wants to Close — Why Spheres Dominate Reality
There is a profound geometric reason why:
- raindrops are spherical
- soap bubbles are spherical
- stars and planets are spherical
- atoms form spherical probability clouds
- galaxies form circular disks
Once curvature exists, it “prefers” to close in on itself.
Not because of an applied force —
but because closure is the lowest-energy, most stable geometric solution to oscillation.
In 3D, curvature closure produces spheres.
In D4, curvature closure produces Spacetime Bubbles (STBs).
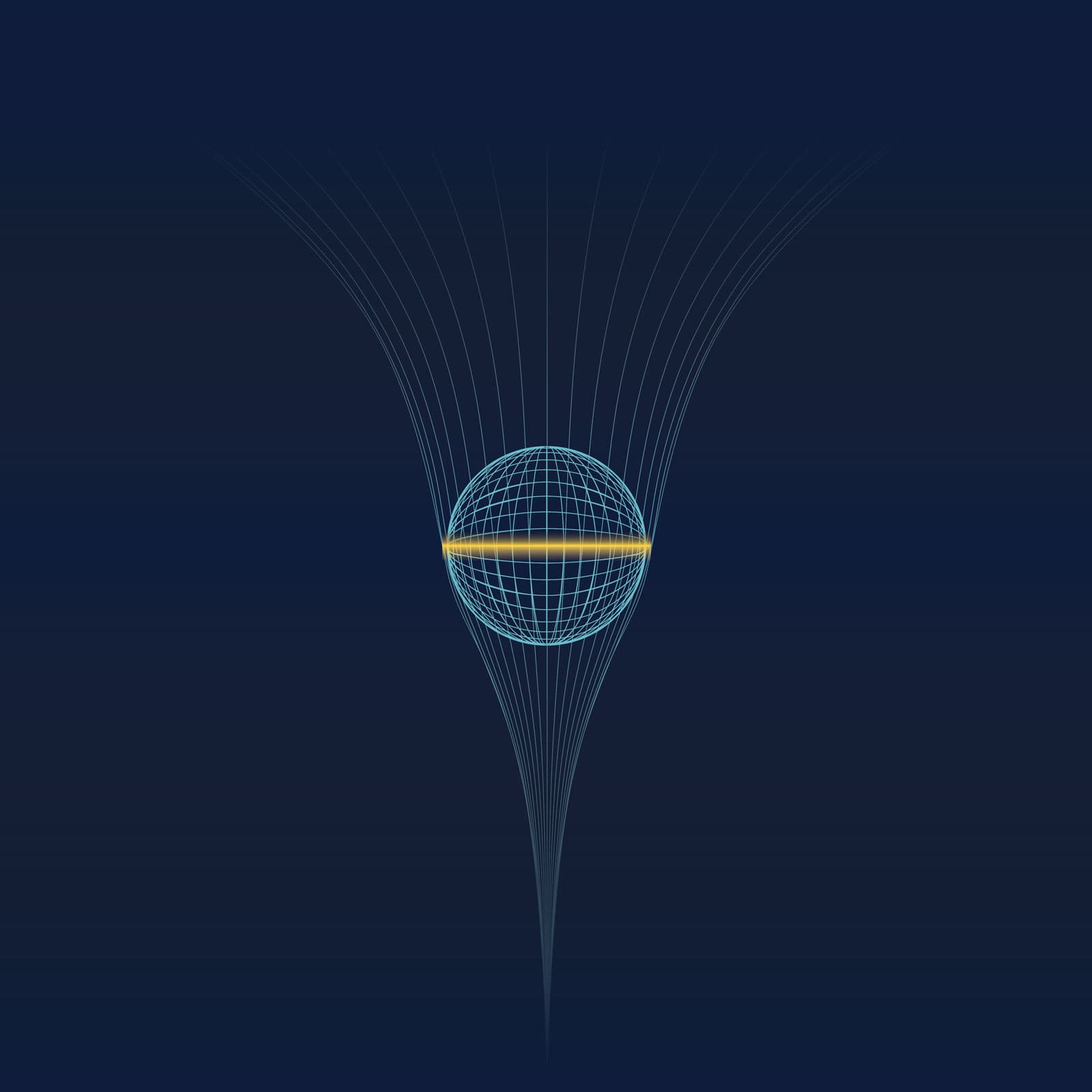
Figure 4.4 — Curvature Closure and Symmetry Preservation
As inward and outward curvature stabilize, closure forms a self-contained geometry with no preferred direction. Rotation distributes curvature tension evenly around the boundary, preserving symmetry and allowing the spacetime bubble to persist.
Once curvature loops completely, the first STB appears — a region with:
- an inside
- an outside
- a boundary
- its own rules
- a local reference frame
This is the birth of structured reality.
Rotation: The Final Stabilizer of Curvature0.
Curvature alone is not stable.
Left unchecked, oscillation would eventually:
- collapse the bubble inward, or
- explode it outward
So a third motion emerges: rotation.
Rotation stabilizes curvature by distributing tension evenly around the bubble.
Rotation is the only motion that:
- has no preferred direction
- has no beginning or end
- preserves the bubble’s shape
- resists collapse and explosion
- converts oscillation into enduring structure
Everything in the universe rotates because rotation is the natural stabilizer of curved spacetime.
The first bubble rotated — and from that moment on, the universe has been spinning itself into existence.
Rotation stabilizes the boundary of an STB by enforcing symmetry; it does not represent internal circulation, transport, or sustaining motion within the bubble.
Rotation is therefore treated as a boundary-condition of the shell geometry, not as a fluid-like spinning of the interior.
Curvature as the Source of Physical Laws
Once curvature exists inside D4, the following become unavoidable:
- Gravity— curvature producing acceleration
- Electromagnetism— curvature forming torsion and waves
- Quantum Mechanics— curvature creating discrete vibrational states
- Particle Physics— curvature forming stable pockets that behave as particles
- Cosmology— curvature guiding expansion, clustering, structure formation
Every physical law begins with curvature.
And from that geometric imbalance, all physical laws unfold.
This is the power of the STB Theory:
It doesn’t assume energy, forces, particles, or spacetime.
It derives all of them from curvature in D4.
Chapter 4 in One Sentence
And curvature itself emerges from the first imbalance in D4
Why All STBs Form at the Same Scale
Once curvature closes and stabilizes, a natural question arises:
Why do spacetime bubbles not form at arbitrary sizes?
The answer follows directly from the defining property of D4.
Every point in D4 is simultaneously infinitely small and infinitely large.
There is no preferred scale embedded in the field.
If a closed curvature structure were smaller than its equilibrium size, inward curvature would dominate and collapse it.
If it were larger, outward curvature would dominate and cause it to disperse.
Only at the exact balance point — the geometric midpoint between infinite contraction and infinite expansion — can inward and outward curvature remain in stable oscillation.
That balance produces a single, self-consistent scale.
At this scale:
- inward and outward curvature are equal
- oscillation neither grows nor decays
- rotation can stabilize the structure
- closure persists without collapse
This is why STBs do not form at many sizes.
They form at one.
Not because the universe selects it —
but because no other size can survive.
Core Structural Assumption — Internal Structure of a Spacetime Bubble (STB)
An STB is not maintained by continuous motion, rotation, or internal flow. Such behaviors cannot survive the extreme formation stress of an STB nor remain stable over cosmological timescales. Instead, the only structure consistent with observed stability, universal size, and long-range interaction is a two-phase standing curvature oscillator confined by a geometric shell. At formation, intense curvature stress excites a resonant mode that becomes trapped within the shell. This mode neither propagates nor decays; it persists as a self-correcting standing oscillation whose resonance defines the STB’s exact equilibrium size. The existence of two coupled phases introduces an intrinsic phase orientation, enabling phase locking between neighboring STBs. Attraction is therefore not a force emitted across space, but a geometric tendency toward phase alignment that minimizes curvature strain. All stable matter, bonding behavior, and cumulative phenomena such as magnetism arise as consequences of coherence, cancellation, or alignment among these standing curvature phases.
Matter exists because curvature can resonate, and attraction exists because resonance prefers coherence.
Chapter 4 — Technical Notes, Clarifications, and Anticipated Objections
The purpose of this appendix is not to argue, but to clarify.
Chapter 4 introduces the geometric origin of curvature, oscillation, closure, and rotation without equations in order to preserve conceptual clarity.
Readers trained in conventional physics may naturally raise questions at this stage.
The most common ones are addressed below.
Objection 1: “This resembles a mechanical ether.”
At first glance, describing D4 as a continuous, tensioned substrate may appear similar to historical ether models.
However, D4 differs in several fundamental ways:
- D4 is not embedded within spacetime
- It does not define absolute rest or preferred frames, or preferred directions
- It does not transmit signals or forces
- It is not directly observable
A preferred direction would violate the defining symmetry of D4 and therefore cannot exist at any level of its dynamics.
Spacetime itself is not something that exists within D4 — it is a stabilized geometric structure that forms from D4.
D4 is therefore not a medium inside the universe; it is the deeper geometric condition from which the universe emerges.
Objection 2: “Why must curvature oscillate instead of settling?”
In familiar physics, curvature can appear static because time, energy conservation, and boundary conditions already exist.
Prior to the formation of a spacetime bubble, none of these conditions are present.
In a continuous, frictionless, boundaryless field:
- imbalance cannot dissipate
- no energy can be lost
- no preferred direction exists
Under these conditions, the only possible response to asymmetry is oscillation.
Oscillation is not assumed — it is the unavoidable behavior of imbalance in a timeless continuous field.
Objection 3: “Rotation seems added rather than derived.”
Rotation is not introduced as an additional mechanism.
It emerges as the only symmetry-preserving stabilization of oscillatory curvature.
Without rotation:
- oscillation grows unstable
- curvature collapses inward or explodes outward
With rotation:
- tension distributes evenly
- no preferred direction forms
- curvature maintains closure
- structure becomes persistent
Rotation is therefore not optional.
It is the only motion compatible with closed, oscillatory curvature in a continuous field.
Objection 4: “This derives physics without mathematics.”
Mathematics describes relationships within a framework.
Chapter 4 establishes the geometric framework itself.
Historically, geometry precedes formalism:
- Euclid came before calculus
- Einstein’s equivalence principle preceded field equations
This chapter identifies the geometric conditions from which physical laws arise.
Later chapters address how familiar equations emerge from these conditions.
Objection 5: “The claims are unfalsifiable.”
The theory makes structural predictions rather than numerical ones at this stage, including:
- universal rotation as a stabilizing principle
- closure as the dominant stable solution
- curvature-defined information storage
- discrete structure emerging from oscillatory geometry
These consequences are examined in later chapters through black holes, quantum behavior, and cosmological structure.
A framework can be testable through its consequences even before its formalism is complete.
Objection 6: “Why four dimensions?”
D4 is not chosen arbitrarily.
Three-dimensional geometry does not naturally support stable, closed, oscillatory curvature without singular collapse.
Four dimensions represent the minimum dimensionality that allows:
- simultaneous inward and outward curvature
- rotational stabilization
- closure without collapse
- persistent structure
D4 is therefore the simplest space capable of producing a stable universe.
Final Clarification
This chapter does not attempt to replace existing physics.
It proposes the geometric origin conditions that make physics possible.
Curvature is not treated as a byproduct of matter or energy.
Matter, energy, spacetime, and forces are treated as stabilized expressions of curvature itself.
The chapters that follow explore how these geometric origins manifest as the physical laws we observe.
© 2025 Michael “Blair” Hopper. All Rights Reserved.

